【コラム】盤面から三つ子 !?　Troika ナンプレ

　ナンプレに関して新たなコンセプトを紹介します。
　完成図から問題を作るというものですが、一風変わったことをしています。
　（難易度：★★★★）

１．「三つ子」という新しいコンセプト

　ナンプレに関して一風変わったコンセプトがあります。
　今回はその話をしてみましょう。

図 1-1

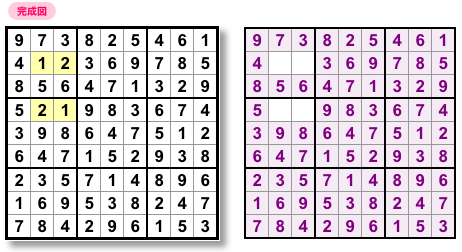
　いきなりですが、ナンプレを３問用意してみました。
　図1-1 です。

　まぁ……普通のナンプレですよね😅
　１つは綺麗な対称形。ナンプレ誌などでは普通に見かける形。
　そして、難易度は激辛ながらも３つとも解ける問題です。
　至って普通のナンプレです。

　しかし、実は、この３つには大きな秘密があります。
　一体どんな秘密なのか？
　合体させるとわかるので、ちょいと合体させてみましょうか。

図 1-2

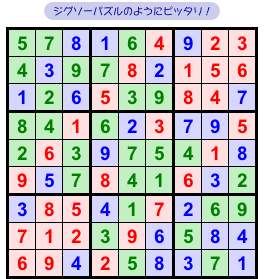
　おおぉ！　ピッタリ！
　ナンプレが完成してしまいました😃
　これが、前図1-1 で述べた大きな秘密なんです。

　詳細を述べましょう。
　こういう仕組みです。

  • 完成図にある81個の数字を３つのグループに分ける。
  • それをヒント数字とみなすと、問題図が３つできあがる。
  • その３問はすべて解ける。つまり唯一解を持つ。

　まるで完成図から三つ子が生まれたような、そんな感じ。
　その「三つ子を作る」というのが、今回のテーマです。

　2022年１月９日。
　ナンプレのフォーラムサイト『The New Sudoku Players' Forum』にて、興味深いアイデアが産声を上げました。
　付けられた名前は「Troika Sudoku」。
　「完成図を３つの問題図に分けることができるか？」という新しいコンセプトが Troika Sudokus. A challenge. というスレッドから誕生しました。

　もちろん、ただ分けるだけではない。
　次のようにクラス分けして美しい Troika も見つけたい、というわけです。

　Magic は普通レベル、Perfect はさらに個数を揃えてグレードアップ、Sublime はさらに美貌も加わって最高級。
　そんなところかな。
　以降は Perfect と Sublime しか現れないので、みなさんはその２種類を頭の片隅においておくと良いでしょう。
　ちなみに、sublime には「崇高な」「至高の」などの意味があります。
　もしかして「完璧」を超えるようなニュアンスがあるのかな？

　あ、「minimal」という新しいワードが出てきましたね。
　これは「余分なヒント数字は無い」という意味です。
　言い換えると「問題図のヒント数字をこれ以上減らすと解けない問題になってしまう」ということです。
　ただ、みなさんは minimal をあまり意識する必要はありません。
　「問題図に無駄がなく洗練されている」くらいの軽い認識でＯＫです。

図 1-3

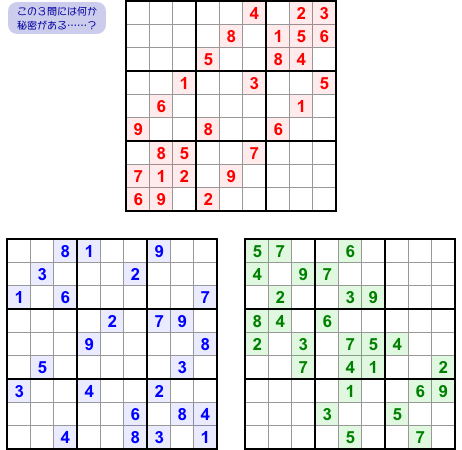
　さて、まずは軽いジャブを１つ。

　Troika Sudoku を考案したスレッド主さんは、提案を投稿した翌日にもう Sublime Troika 寸前の物を披露していました。
　図1-3 です。
　おぉ〜、みんな綺麗に左右対称🥰
　美人の三姉妹ですわ🥰

　ただ、残念ながらこれらは３つとも minimal ではありません。
　どれもヒント数字を何個か取り除いても解けてしまうというシロモノです。
　だから Sublime 寸前。
　本当に惜しい！

　でも、逆に言えば、もぅ既にゴール近くまで来ているということです。
　あとは minimal というハードルをクリアすればいい。

　Troika Sudoku というアイデアが提案されたそばから、もぅ最高級レベルの傑物が見つかった。
　これだけ早いと Sublime Troika の期待は高まって、すぐに見つかって議論が終わっちゃいそう？
　果たして、議論の行方はどうなるか。

２．Perfect、発見！

　いや〜、ホントに議論がすぐに終わりそうです😅
　先述の Sublime 寸前の Troika が投稿された翌日、Perfect Troika が投稿されてしまいました。

図 2-1

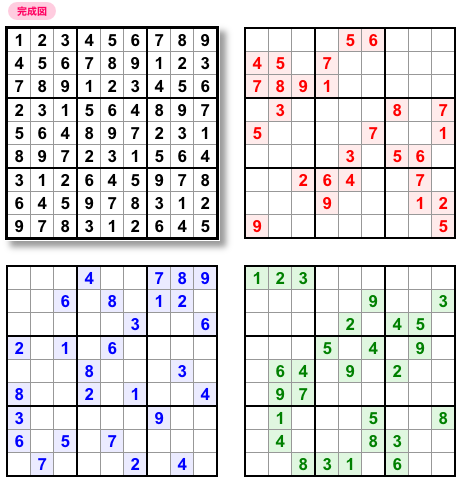
　しかも、その発見者さんは Perfect Troika を４組も見つけてた。
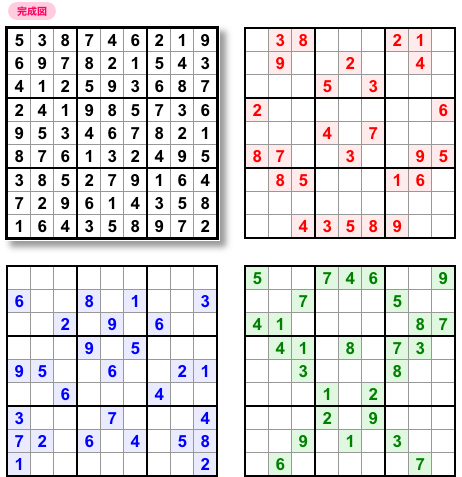
　図2-1 はその中の１つです。

　81個の数字が27個ずつに分かれている。
　どのナンプレも唯一解を持っていて、minimal である。
　しかし、対称形ではないから Sublime には届かない。
　ものの見事に Perfect Troika です。

　親記事投稿から３レス経ったらもぅ Perfect。
　登山で言えばもぅ８合目。
　あまりに健脚すぎやしませんか？😅

　……とまぁ、ここまで読むといとも簡単に Perfect Troika が発見されたように見えますね。
　しかし、実際はそんなことはありません。
　実は、３分割で問題図を作るにあたってかなりの困難が待ち受けていました。

　その困難を説明するために、まずはナンプレの作り方について話をしましょう。
　ナンプレの作り方はいくつかありますが、その中の１つに「完成図から数字を消す」という方法があります。

図 2-2

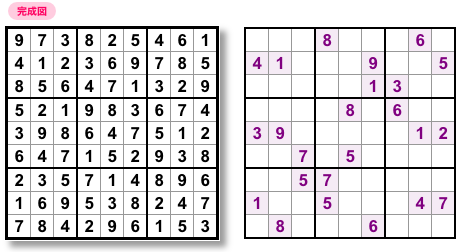
　実際に問題を作ってみました。
　図2-2 左側の完成図を用意し、そこから24個の数字を選び、他のマスの数字をすべて消す。
　そうしてできたのが 図2-2 右側の問題図です。
　もちろん、ちゃんと解けます。

　単に「ナンプレの問題を作る」という点では、この方法は非常に簡単です。
　数字をたくさん残しゃぁいいんだもの😅
　ヒント数字が40個も50個もあれば、まぁ高確率で唯一解を持つでしょう。
　完成図を作ってしまえば、問題はもぅ８割方できたも同然なんですね。

　前図2-1 の発見者さんは、この数字消去法で Troika を作ることを考えました。
　大まかな方針は、まずは特殊な完成図を用意し、その完成図から数字を27個選んで第１の問題図を作り、残り54個の数字から27個選んで第２の問題図を作り、最後に残った27個が第３の問題図になる。そういう要領です。
　これで３問とも唯一解を持って minimal な問題図であれば、晴れて Perfect Troika 完成！ ……となるわけですね。
　「特殊な完成図」については、図2-4 で後述しましょう。

　ただ、残念ながらこの数字消去法にはいくつかの欠点がある。
　製作者のアイデアや作意を盛り込めない。見た目美しい問題図にしにくい。etc...
　特に、Troika 作成に関しては次の欠点が強烈なハードルとして立ち塞がるんです。

そこそこ数字を残しても、唯一解を持ってくれないことが多い。

　中級程度のナンプレ問題には24個程度の数字が配置されています。
　しかし、上記の方法で数字24個の問題を作るというのは結構大変です。
　なんせ、テキトーに数字を残して問題図を作っても「数字が１マスも埋まんねぇ😅」なんてことはザラにある。
　数字選びには試行錯誤が山ほど必要なんですね。
　（事実、図2-2 の問題作成には結構な時間がかかった）

　唯一解を持ってくれない理由はあります。
　ナンプレの完成図には次の厄介な性質があるからです。

どの完成図にも「別解のタネ」がそこら中に潜んでいる。

図 2-3

　実は、ナンプレの完成図には「別解の起こり得る数字配置」が必ず存在します。
　例えば、図2-3 の黄色４マス。
　この４マス以外をすべて抜き出して極端な問題を作ってみたけれど、こんなにも大量のヒント数字があるのに別解が生じてしまう。
　空きマスには数字１か２を入れることができるけど、入れ方が１２２１でも２１１２でもナンプレは完成できちゃいますもんね。
　この黄色４マスは別解のタネの１つです。

　一般的なナンプレの完成図は数字が不規則に並んでいます。
　だから、タネは形も大きさも多種多様。
　図2-3 のような４マスの物は最小で、６マス以上のタネもたくさんある。
　２種類の数字をすべて含む大量18マスのタネもある。
　盤面にもよるけれど、こういったタネは盤面に300〜500個ほど分布しています。
　どこにどう散らばっているのかわからないタネ達を１つも残さず排除して問題図を作るというのは、まぁ〜それはそれは大変なんですね。
　ましてや、Troika 作成となれば苦労は３倍。至難の業なんです。

　ただ、ここでちょっとだけ朗報がある。
　実は、すごく単純なタネ分布を持つ完成図が存在します。

図 2-4

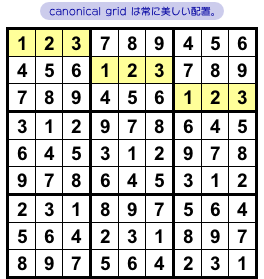
　それが 図2-4 です。
　この盤面、なんとな〜く数字が綺麗に整列してるっぽく見える。
　その見た目通りの大きな特徴があります。

　ブロック３個並んだヨコ長３×９マス領域を見てみましょう。
　その領域をブロック単位で見ると、１２３はトリオのまま斜めに移っていますね。
　４５６も７８９も同様にトリオを保っている。
　タテ長９×３マス領域も同じ。１４７、２５８、３６９が仲良くトリオ。
　数字の並びがすごく単純でわかりやすい！

　このように、どの３×９領域（タテ長ヨコ長問わず）にもトリオが必ず３回ずつ現れている盤面が存在します。
　これを canonical grid と呼びます。
　これは most canonical grid と呼ばれることもあり、MC grid という略称も存在します。
　当ページでは MC グリッド と呼ぶことにしましょう。

図 2-5

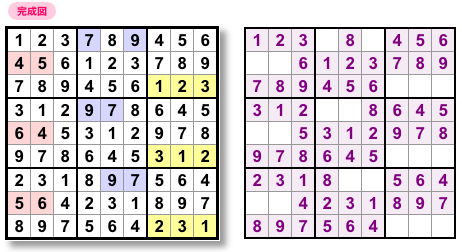
　さて、この MC グリッド。
　数字の並びが単純だと言いましたが、これは一体何を意味するのか？
　それは、こういうことなんです。

別解のタネも並びが単純になる。
そのおかげで、小型のタネが急増する。

　図2-5 の赤色や青色のように、タネの大半は３列に単純に並びます。
　そのようなタネは最大でも９マスで、その場合は必ず「三」の字になる（黄色）。
　盤面にはハンバーガーアイコンのような小さいタネが規則的に分布する。
　こういう特徴があるわけですね。

　実は、図2-1 の完成図は MC グリッドです。
　図2-1 の発見者さんは「小型のタネを多数持つ完成図の方が Troika を見つける可能性が高い」と予感していたそうで、MC グリッドに目を付けていました。
　その予感は正解だったようですが、それでもタネが盤面に大量に存在することは変わらず、Perfect Troika の作成は非常に手間のかかる作業でした。
　事実、成功までに膨大な試行錯誤を経ています。
　１つの MC グリッドからヒント数字27個の問題図（唯一解を持ち minimal な物）を大量に作り置きして、それらを使って作業をした。
　最初は30万個だったストックを300万個にまで広げ、Troika 発見に精力を注いでいましたね。

　具体的な方法は、数字を１マスも共有していない問題図２つをストックから探しました。
　そのペアは54マスを占有しますが、完成図からその54個の数字を消すと第三の問題図ができあがります。
　それが唯一解を持ち、かつ minimal であれば、めでたく Perfect Troika の完成となるわけです。
　これを該当ペアすべてに対して調べたわけですが、なんと、ペアの総数は2000万組を超えていたという！

　一連の作業をすべてコンピュータに任せるのは当然としても、気が遠くなる作業なのは間違いない。
　実際、その300万個の中から見つかった Perfect Troika はたったの104組だったそうです。
　まるで砂金採り😅

　ちなみに、当の発見者さんは MC グリッドでない盤面に対しても同じ挑戦をしていました。
　そして、諸々の調査の結果、次の推測に至ったようです。

　必ず大量に砂金が見つかる砂金採り。
　こう聞くと、すっごく夢が広がるね😅

３．美しい Troika 達

　Troika の議論が進むにつれ、スレッドにはたくさんの例や考察が寄せられました。
　その中で美しい形の Troika（図3-1 を除く）も生まれたので、ちょいとご紹介。
　このセクションは、文章を読むより図をパパッと見ていってください😊

図 3-1

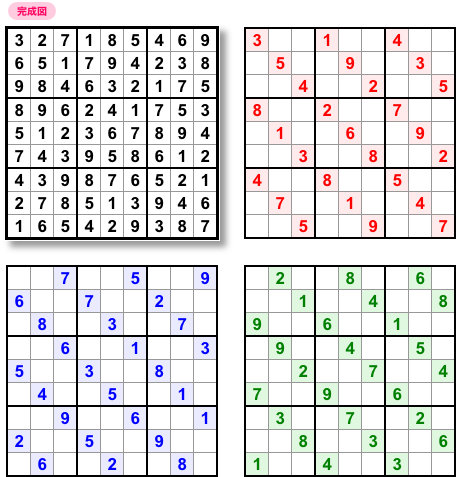
　いや〜、いきなり美しすぎる形🥰
　しかし、残念ながらこれは Suplime Troika にはなれませんでした。
　３問とも minimal ではないからです。

　ただ、３問合わせても余分なヒント数字はたった４個しかありません。
　だから本当に惜しかった。

図 3-2

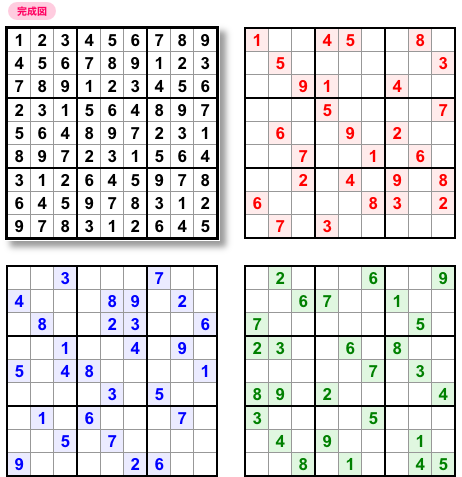
　図3-2 はナンプレ上級者なら理解できる Perfect Troika です。
　この３問、すべて本質的に同じ問題図です。
　外見は違うけど性格がまったく同じ三つ子、といったところでしょうか。

　次の４つを施しても本質的に同じ構造の盤面ができあがる、ということがナンプレ界では知られています。

  • 数字を置換する。
  • band を置換する。または stack を置換する。
  • band 内のヨコ列を置換する。または stack 内のタテ列を置換する。
  • 盤面を回転・裏返しする。

　ちなみに、本質的に同じ構造であることを数学では「同型」と言います。
　Troika スレッドの内部では「isomorphism」という単語が割と現れて、数学の視点でも議論が活発に行われているんですね。

図 3-3

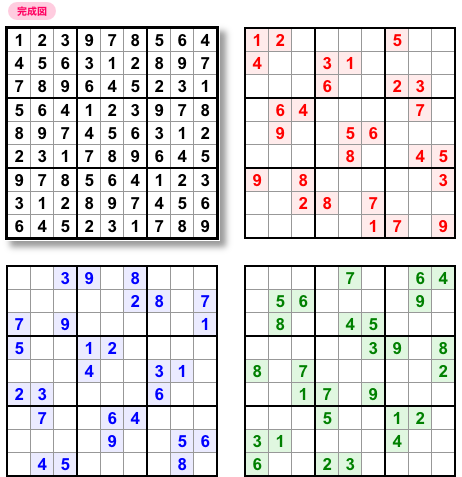
　そして、ついに Sublime Troika 現る！

　この３問はヒント数が27個であり、対角線で線対称になっています。
　ついでに言うと、前図3-2 で説明した「同型」でもあります。

　よく見ると、どのタテ列・ヨコ列・ブロックにも数字が３個ずつありますね。
　あちこちで数字がＬ字に並んでいて見た目も模様のように綺麗🥰
　Troika の議論の最終結論と位置づけても良いかもしれませんね。

４．さらに苦難の道へ……

　Troika の活発な議論が行われているさなか、実は、１つの提案が起きていました。

完成図を４つの問題図に分けることはできますか？

　なんと、子供をもう１人増やせという！
　今まで Troika 発見に燃えていた猛者達はこの四つ子を「Quadriga」と名付け、さらに苦難の道を歩んでいくのでした。

図 4-1

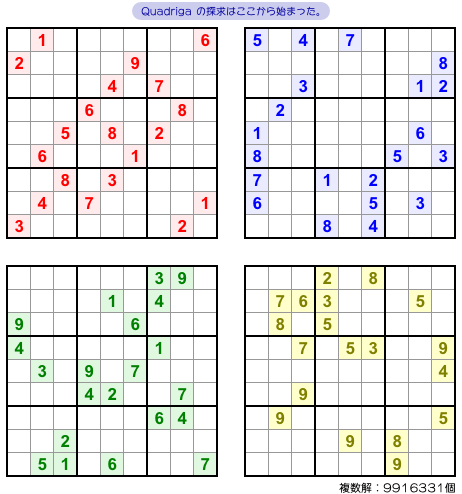
　議論の場は Quadriga Sudoku という新しいスレッド。
　そのスレッド主さんは、まず手始めに自分の成果を５組披露しました。
　そのうちの１つが 図4-1 です。

　完成図がちゃんと４つに分割されている。
　これで Quadriga 完成か……と思いきや、図の右下に何やら巨大な数値が書かれている。
　この数値、解の個数です。
　黄色の問題図は唯一解を持っていない。なんと 9916331 個の解がある！
　他の３問にしっかり唯一解を持たせたら、こんなにも黄色にしわ寄せが来ちゃってた😅

　そういや、セクション２ではナンプレの作り方・数字消去法の話をしましたっけ。
　数字をたくさん残しても唯一解を持ってくれないことが多いわけです。
　なのに、四つ子に求められるヒント数は平均で 81÷4＝20.25 個。
　Perfect Troika の27個ですら別解の山を築いていたのに、今度は「さらに少ないヒント数で唯一解を持て！」と言ってきた。
　もはや無謀な要求である😅

　しかし、そこはナンプレフォーラムの猛者達、991万個から個数を驚異的に減らしていく。
　15000個、7000個、2600個、516個、そして、ついに「２個」にまで到達した。
　ゴールテープまで本当にあと一歩という躍進を見せたのです。

図 4-2

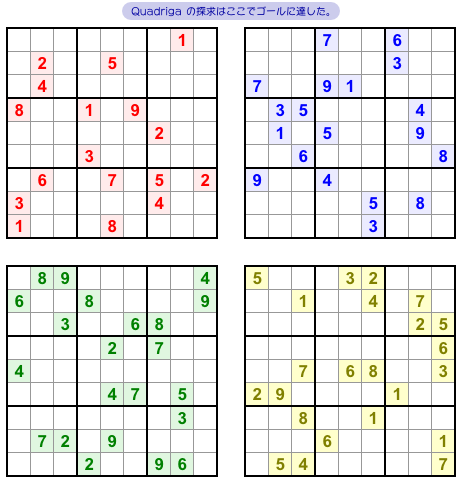
　結論を言うと、Quadriga の発見は成功しました。
　図4-2 です。
　問題図のヒント数字はそれぞれ 17個, 19個, 22個, 23個。
　どれも解ける問題です。

　Quadriga を作る基本方針は、「なるべく少ないヒント数の問題図を先に作る」です。
　最初に苦労しておけば後がラクになる、と似たようなものかな？
　最初の２問はヒント17〜19個程度で作り、残りの数字達を分割して２問同時に作るという手法をとりました。

　その手法は基本に忠実、とにかく地道なものでした。
　与えられた完成図からヒント17個の minimal な問題図をすべて作る。ヒント18個の物もすべて作る。19個以降も同様。各個数ごとに問題図のストックを用意した。おそらく22個くらいまで用意した。
　そして、数字を１マスも共有しない問題図２つをストックから見つけ、残りの数字から別の２問を探していきました。
　図4-2 で言うと、赤色＆青色の問題図をストックから見つけ、残り45マスの数字を試行錯誤で二分しまくって緑色＆黄色を見つけたわけです。

　もちろん、Troika と同じく「別解のタネ」に大いに悩まされながらの道のりでした。
　その分、スレッドではタネに関する濃い定理も導かれてましたね。
　「最小の別解のタネは４マス。そのタネは１マスずつ４問に分散されなきゃいけない」
　「図4-1 で言えば、赤色＆青色を抽出した後の残りは45マス。45マスを二分しなきゃいけないから、45個のうちどの数字１個を除去しても解ける問題でなければいけない」
　定理の内容が難しいのでここでは説明しませんが、興味のある方々は当該スレッド Quadriga Sudoku をご覧ください。
　とにかく、彼らは濃い議論を交えながらも道なき道を邁進していたということです。

　そんなこんなで、盤面からめでたく四つ子ができた。
　三つ子・四つ子が成功したとなると、やっぱり「五つ子」なんてものも気になりますね。
　果たして、五つ子は可能なんだろうか？

　結論を言うと、残念ながら五つ子は絶対にできません。
　次の定理が知られているからです。

　完成図を５分割すると、ヒント16個以下の問題図が必ずできちゃうんです。
　ヒント数の平均は 81÷5＝16.2 だから、どれかの問題図はヒント16.2個以下ですもんね。

　この定理は2012年発表の論文で証明されています。
　セクション２で触れた「別解のタネ」に注目して複数解を考察し、それを活かしてコンピュータで定理を導いています。
　この論文（2013年９月改訂版）は学術記事サイト『arXiv』のこのページでダウンロード可能です。
　興味があれば是非。

　五つ子以降がダメなら、逆に「双子」はどうか？
　たぶん、これは議論する余地はほとんどなさそう。
　試行錯誤で40個と41個に分ければ、まぁどっちも解ける問題図になっていそうです。
　しかし、どっちもヒント数字が大量だから、たぶん minimal にはなってなさそうです。
　双子は……無理かな？
　troika, quadriga ときたら双子は「biga」になるんだろうけど、ナンプレ界には Biga は存在できなさそうです。

参考・参照

更新履歴