なぜ２つの領域内部の数字が一致するのか？

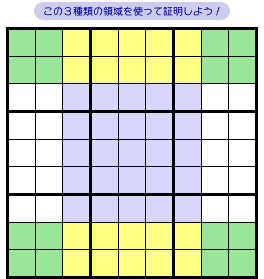
　まずは 図1-1 を用意しましょう。
　この盤面の状況は以下の通りです。

• 緑色領域は従来通り。４ブロック内部で４マスずつ矩形状に並んでいる。
• 青色領域は中を塗りつぶして５×５の矩形にしておく。
• さらに、２つの領域に接する位置に黄色領域も付け加える。

　緑色領域は16マス、青色領域は25マスあることに注意してください。

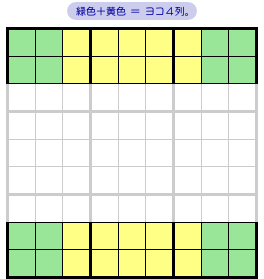
　まず、緑色＋黄色 の領域に注目しましょう。

　図1-2 の通り、これはヨコ４列を形成していますね。
　だから、緑色＋黄色 には 数字１〜９が４個ずつ 入ることがわかります。
　当ページでは、これを単純に 数字が４セット入る と言うことにしましょう。
　もちろん、９個の数字１〜９をひっくるめて「１セット」です。

　というわけで、こうなりました。

• 緑色＋黄色 ＝ 数字４セット。

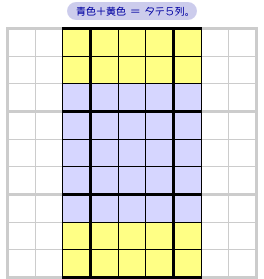
　次は、青色＋黄色 に注目します。

　図1-3 の通り、これはタテ５列を形成しています。
　だから、青色＋黄色 には 数字が５セット入る ことになりますね。

　というわけで、こうなりました。
　ここでは、わざと５セットを 4＋1 と分けておきましょう。

• 青色＋黄色 ＝ 数字４セット＋数字１セット。

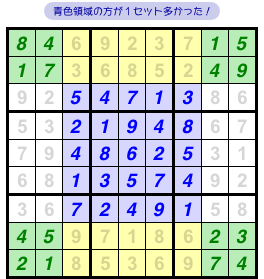
　ちょいと試しに、具体的な盤面で確認してみましょう。
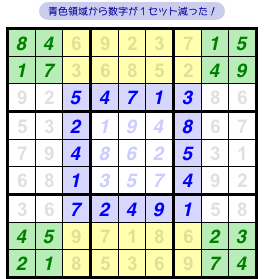
　図1-4、緑色領域と青色領域のメンバーをそれぞれ数えてみると……、

数字	１	２	３	４	５	６	７	８	９
緑色領域	3個	2個	1個	4個	2個	0個	2個	1個	1個
青色領域	4個	3個	2個	5個	3個	1個	3個	2個	2個

　おぉ！
　どのメンバーも青色領域の方が１個だけ多い！
　青色領域のメンバーは、緑色領域よりもちょうど１セット多いんですね。

　ここまでわかると、結論まであと一息！
　青色領域から中央ブロックをくり抜きましょう。

　中央ブロックを抜き取ると、青色領域は数字を１セット失います。
　ということは……？
　緑色領域と青色領域のメンバーは完全一致する、ということになるんです。