1.ルール
まずは、サムクロスのルールを説明しましょう。
既にご存じの方はセクション2に進んじゃってください😊
サムクロスのルールは3つあります。
次の【1】【2】【3】ですね。
「区切られた一列」とは、白マスが連続している一列のことです。
青色や赤色などで示した一列を指します。
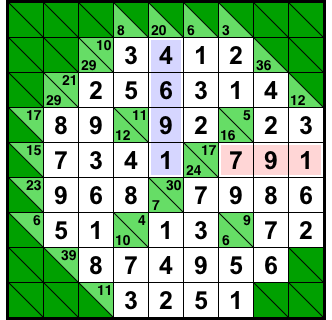
図1-1 はサムクロス完成図ですが、たしかにどの列もルールに従っていますね。
数字の合計は正しく、各列の中の数字はすべて異なります。
最初に空きマスだらけの盤面が与えられる。
そして、ルールに沿って空きマスに数字を確定させ、盤面を完成させていく。
サムクロスはそういうパズルです。
そして。
サムクロスを解くにあたって絶対に欠かせない物があります。
それは 唯一パターン です。
マス数と合計値によっては、マスに入り得る数字の組み合わせがただ1つに決まります。
このことは非常に大きな手掛かりになるので、是非とも覚えておくべし!
詳細は サムクロスのルール をご覧ください。
2.最も簡単な例・その1
サムクロスの問題図には合計値しか書かれていません。
が、実は、合計値によっては白マスに入る数字が制限されるんです。

図2-1、上部の青色3マスを見てみましょう。
2マス同士の交差で、こういう状況です。
- タテ列・ヨコ列ともに2マスで構成されていて、その2列はマスAで交差している。
- 一方は合計3の唯一パターン。他方は合計11である。
もしかしたら、ここでふと気付いた方々は居るかもしれない。
「2マス合計3」は唯一パターンで、マスAには1か2しか入らない。
なのに相手は 2マス合計11。
数字1や2の立場からすると、合計11はずいぶん大きい気がするなぁ……。

実際その通りで、そこには結論が1つ生まれるんです。
- マスAに数字2が確定する。
なぜでしょう?
それは、合計11の2マスには数字1を入れられないからです。
もしマスAに1を入れてしまうと、その右隣のマスには10を入れなきゃいけなくなる!
もちろんルール【1】はそんなの認めてくれません😅
というわけで、上記の結論に至るんですね。
その後は、残りの青色マスにも数字が確定。
3マスすべて埋まりました😄
実は、同じ理屈の成り立つ箇所があと2つあります。
それも紹介しましょう。
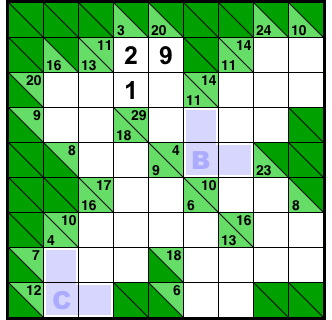
図2-3、青色6マスです。
交差箇所をそれぞれB, Cとしておきましょう。
- 中央付近は合計4(唯一パターン)と合計11の交差。
- 左下隅は合計4(唯一パターン)と合計12の交差。
マスB, Cには最大でも3しか入らないのに、相手は合計11と12。
やたら大きい。
2マスとも数字が確定しそうですね。

実際、確定します。
- マスB, Cともに数字3が確定する。
理由は 図2-2 と同じです。
マスBやCに数字1を入れてしまうと、ルール【1】に抵触してしまうからですね。
要は、「2マス合計11以上」という時点で、数字1はもぅ入れられないんですね。
このように、大きな合計値に対しては数字の可能性が狭まります。
こういうのもサムクロスを解く手掛かりになるんですね。
2マス・合計3&11。
2マス・合計4&11。
2マス・合計4&12。
この3つは初歩的な形です。
できればこの形も覚えておきたい……が、覚えるのは大変かもしれない。
もし覚えにくい時は、唯一パターン(合計3・合計4)の側から攻めてみるのも良し!
交差箇所に入る数字は二択に絞られるから、「もし1だったら……?」「3だったら……?」と1個ずつ試してみる。
これも1つの手です。
3.最も簡単な例・その2
前セクション2では、小さい合計値の場合を解説しました。
次は、大きい合計値で同じことをやってみましょう!

図3-1、青色の3マスです。
状況は次の通り。
- 2マス同士の2列がマスAで交差している。
- 一方は合計17の唯一パターン。他方は合計9である。
今度は前セクションとは逆です。
「2マス合計17」は唯一パターンで、マスAには8か9しか入らない。
なのに相手は 2マス合計9。
数字8や9の立場からすると、合計9は絶対小さいよなぁ。
そんな感想を抱いてしまう。
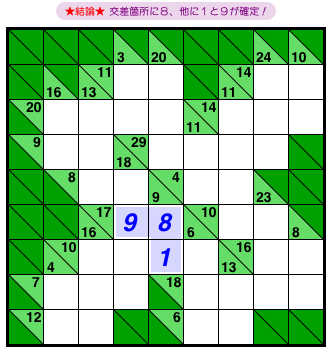
その感想通りの結論が待っています。
- マスAに数字8が確定する。
なぜこうなるんでしょう?
それは、合計9の2マスに数字9を入れられないからです。
もしマスAが9だと、その下のマスは0になってしまう!
そんなんではルール【1】からお仕置きを食らっちゃう😅
というわけで、上記の結論に至るんですね。
その後は、残りの青色マスに1と9も確定。
3マス綺麗に確定しました😄
前セクションと同様に、同じ理屈の成り立つ箇所があと2つあります。
それもご紹介。
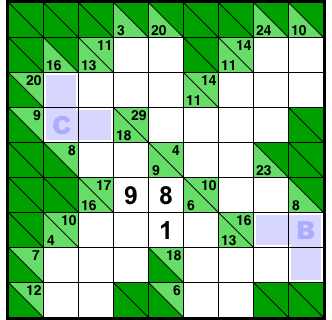
図2-3、青色6マスです。
交差箇所をそれぞれB, Cとしておきましょう。
- 右下隅は合計16(唯一パターン)と合計8の交差。
- 左上隅は合計16(唯一パターン)と合計9の交差。
マスB, Cには最小でも7しか入らないのに、合計8や9は小さい。
ここも数字確定の匂いがしています。

まさにその匂い通り!
- マスB, Cともに数字7が確定する。
理由は 図2-2 と同じです。
マスBやCに数字9を入れてしまうと、ルール【1】でマズいことになっちゃう……。
当然すぎる話ですが、合計値以上の数字は入れられません。
例えば「合計6」の列には6以上の数字はNGなのです。
この話を知っているだけで、このセクションの話は簡単に理解できますね😄
2マス・合計16&8。
2マス・合計16&9。
2マス・合計17&9。
この3つも初歩的な形です。
できればこの形も覚えておきたいところ。
もし覚えにくい時は、唯一パターン(合計16・合計17)の側から攻めてみましょう!
交差箇所の数字は二択に絞られるから、試しに数字を入れてみれば「あ、9だと合計を超えちゃうわ😅」とすぐにわかります。
4.唯一パターンのマスが多くても理屈は同じ
この解法のキモは「大きすぎる/小さすぎる数字をうっかり入れると、隣のマスにはおかしな数字が入っちゃう😵」というところです。
そして、このことは唯一パターン側の列が長くても成り立つんです。
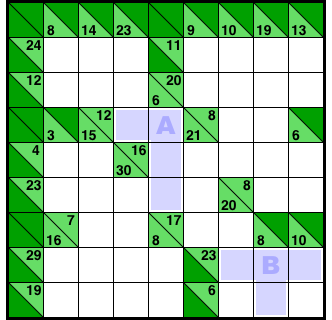
図4-1、2マスと3マスの列が交差しています。
交差箇所をそれぞれA, Bとしましょう。
どちらも3マス側は唯一パターンです。
- 中央付近は合計12と合計6(唯一パターン)の交差。
- 右下隅は合計8と合計23(唯一パターン)の交差。
3マスの列が出てきましたが、実は理屈は変わりません。
マスAは3以下なのに、合計12はずいぶん大きい……。
マスBは6以上なのに、合計8はやたら小さい……。

結論はこうなります。
- マスAに数字3が確定する。
- マスBに数字6が確定する。
理由は同じです。
マスAが1や2だと、左隣のマスは10以上になっちゃう。
マスBが8や9だと、下のマスは0以下になっちゃう。
こういうわけですね。

最後に例をもう2つ。
図4-3 の2カ所です。
- 右上隅は合計13と合計11(唯一パターン)の交差。
- 左下は合計7と合計30(唯一パターン)の交差。
結論はこうなります。
- 交差箇所のマスに数字5と6が確定する。
説明は省略します。
皆さんで確かめてみてください。
あっ、もちろん、数字8と1も確定します😃
更新履歴
- 2024. 7.29.
- 新規公開。