1.素数を小さい順に並べるだけ
皆さんご存じの一般的な魔方陣を基に、小さい順に素数をそのまま配置するだけ!
長さ9の素数等差数列 \(199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879\) なら、下図の通りです。
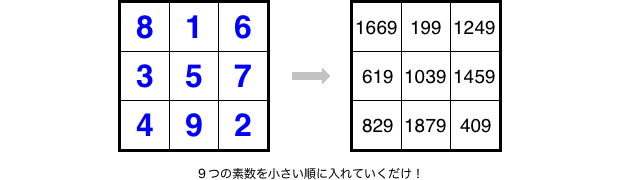
青色数字を番号とみなして、番号順に入れていくだけでいいんです。
実に簡単!
もちろん、長さ16や25の等差数列が見つかれば、4×4や5×5サイズの魔方陣も可能です。
ただ、小さい素数からなる長い等差数列は……まぁ〜見つからん!
パソコンでザッと調べてみたけれど、1000万までの素数に対しては長さ13が最大でした。
長さ12ならポツポツ見つかるものの、長さ13はかろうじて3個見つかっただけ。
しょーがない。
Webサイト『Primes in Arithmetic Progression Records』に助けを求めよう!
そのサイトには長い素数等差数列の記録が並んでいます。
その中からできるだけ小さい素数を探したら、なんと長さ16の等差数列を発見しました。
まぁそれでも9桁ですが😅
素数のみからなる、長さ16の等差数列。
\(p_n=53297929+9699690(n-1)\)
\((n=1, 2, \cdots, 16)\)
さぁ、これで4×4の素数魔方陣を作れますね!
実際に作ってみましょう!
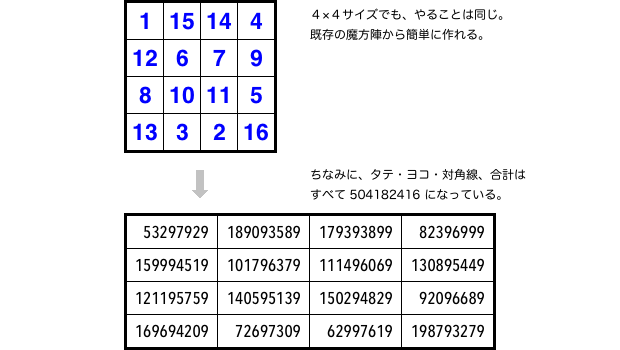
9桁でも結構迫力があるモンです😅
でも、やっぱり ID番号か何かにしか見えない😅
魔方陣っぽくない😅
2.なぜ小さい順に並べるだけで良いのか?
なぜ前セクションの方法で魔方陣ができあがるんでしょう?
それは、本編のセクション2と同じ理屈が通用するからなんです。
本編に倣うと「1を引いて6で割る」という操作をすることになるけれど、ここでは別の数値を使います。
等差数列 \(199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879\) は、初項 \(199\), 公差 \(210\) ですね。
そこで、元の素数魔方陣の各数値から199を引いてさらに210で割ってみる。
そうしたら、ものすごい簡素な魔方陣に大変身するんです。
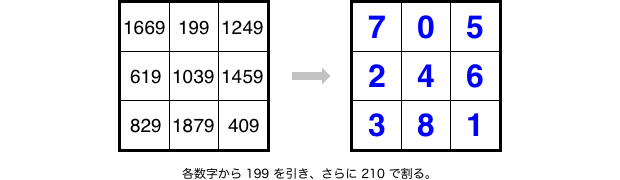
あとは、青色数字の魔方陣から「210倍して199を足す」と逆操作を施せば、元の素数魔方陣を復元できますね。
ところが。
盤面をよ〜く見ると、逆操作を使うまでもないことがわかる。
- 最初の素数 \(199\) は0のマスに入れる。
- 2番目の素数 \(409\) は1のマスに入れる。
- 3番目の素数 \(619\) は2のマスに入れる。
(中略) - 最後の素数 \(1879\) は8のマスに入れる。
青色数字が単なる番号と化しているんですね。
だから、ただただ素数を0番から順に入れていけば良い。
前セクション1の手法と本質的に同じであり、この手法で事足りるんです。