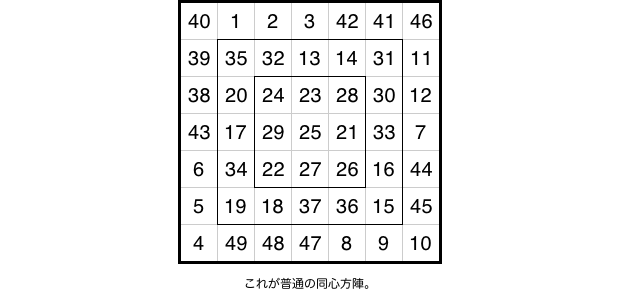
1.3×3魔方陣に拡張させる場合
本編ではこう述べました。
- 盤面中央に素数 \(5437\) を置いたなら、和が \(5437\mspace{-2mu}\times\mspace{-2mu}2\) である素数ペアを周りに巻き付けなきゃいけない。
そうしないと同心方陣はできない。
この理由を説明しましょう!
まず、1マスに素数 \(5437\) を入れて、それを中心として3×3素数魔方陣に拡張することを考えます。
下図のように、周り6マスに入る素数をそれぞれ \(a,\ b,\ c,\ d,\ e,\ f\) とおきましょう。
もちろん、どの列も合計値は等しいという前提だから、その値を \(S\) としておきます。
うまく \(S\) の値が判明すれば万々歳ですね!
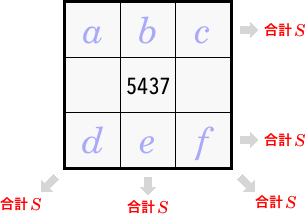
まず、ヨコ2列について簡単に成り立つ等式が1つ。
\[ a+b+c+d+e+f = 2S \tag{1} \]そして、 \(5437\) を含むタテ列と対角線については
\begin{align} a+f+5437 &= S \\ b+e+5437 &= S \\ c+d+5437 &= S \end{align}が成り立ちますが、この3式は次の \((2)\ (3)\ (4)\) に変形しておきましょう。
\begin{align} a+f &= S-5437 \tag{2} \\ b+e &= S-5437 \tag{3} \\ c+d &= S-5437 \tag{4} \end{align}この \((2)\ (3)\ (4)\) を \((1)\) に代入すると、
\[ (S-5437)+(S-5437)+(S-5437) = 2S \]
となり、この式を整理すれば \(S=5437\times3\) が得られます。
おぉ、合計値 \(S\) が判明した!
\(S\) の値がわかったから、\((2)\ (3)\ (4)\) の右辺を計算できますね。
\begin{align} a+f &= 5437 \times 2 \\ b+e &= 5437 \times 2 \\ c+d &= 5437 \times 2 \end{align}この3式から、次のことが判明しました。
- 和が \(5437 \times 2\) である素数ペアが \(5437\) の周りに巻き付く。
具体的には下図の通りです。
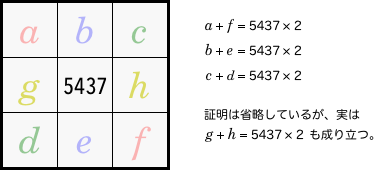
というわけで、必ず「和 \(5437 \times 2\)」を意識して3×3の素数魔方陣を作ることになります。
もちろん「\(a+b+c=5437 \times 3\)」など外周4列にも気をつけて、慎重にペアを選びましょう。
一例はこんな感じです。

2.5×5魔方陣に拡張させる場合
セクション1では、うまく3×3魔方陣ができました。
それを5×5に拡張させるには何が必要でしょうか?
同じように素数ペアの和が \(5437\mspace{-2mu}\times\mspace{-2mu}2\) でなきゃいけないんだろうか……?
まず、前セクション1の3×3魔方陣はどの列も合計値が \(16311\) であることに注意しましょう。
また、9マス全体の合計は \(48933\) です。
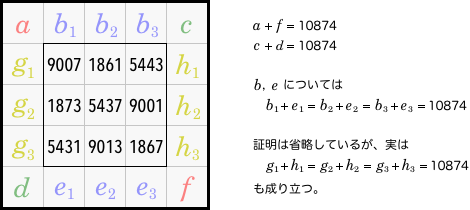
1と同様に、3×3魔方陣の周りを \(a,\ b,\ c,\ d,\ e,\ f\) とおきましょう。
ただし、\(b,\ e\) は3マスの合計値を表します。
また、一列の合計値を \(S\) としましょう。
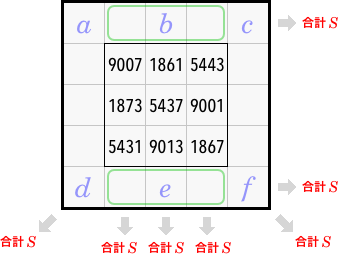
まず、ヨコ2列について簡単に成り立つ等式が1つ。
\[ a+b+c+d+e+f = 2S \tag{5} \]そして、対角線については
\begin{align} a+f+16311 &= S \\ c+d+16311 &= S \end{align}さらに、3×3魔方陣をまるごと含むタテ3列については
\[ b+e+48933 = 3S \]が成り立ちますが、この3式は次の \((6)\ (7)\ (8)\) に変形しておきましょう。
\begin{align} a+f &= S-16311 \tag{6} \\ c+d &= S-16311 \tag{7} \\ b+e &= 3S-48933 \tag{8} \end{align}この \((6)\ (7)\ (8)\) を \((5)\) に代入すると、
\[ (S-16311)+(3S-48933)+(S-16311) = 2S \]となり、この式を整理すれば \(S=27185\) が得られます。
\(S\) の値が判明したから、式 \((6)\ (7)\ (8)\) はさらに計算できますね。
\begin{align} a+f &= 10874 \\ c+d &= 10874 \\ b+e &= 32622 = 10874 \times 3 \end{align}この3式から、こういうことが判明しました。
- 和が \(10874\)(\(=5437\mspace{-2mu}\times\mspace{-2mu}2\))である素数ペアが3×3魔方陣の周りに巻き付く。
具体的には下図の通りです。
\(b,\ e\) についてはさらに詳しいことがわかります。
というわけで、必ず「和 \(10874\)」を意識して5×5の素数魔方陣を作ることになります。
もちろん「\(a+b_1+b_2+b_3+c=27185\)」など外周4列にも気をつけて、慎重にペアを選びましょう。
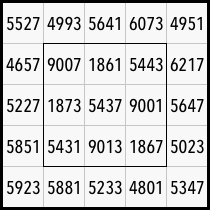
一例はこんな感じです。
前セクションと当セクションで証明を展開しましたが、実は、筋道は本質的に同じです。
そのため、5×5からも同じ理屈が通用し、いくらでも拡張可能です。
本編の魔方陣は13×13サイズにまで拡張された傑作です。
上記の証明は一般論ではなく、盤面中央が \(5437\) である素数魔方陣に対するものです。
しかし、これは素数魔方陣に限った話ではなく、どんな同心方陣にも当てはまります。
盤面中央に数字 \(x\) を置いたなら、和が \(2x\) である数字ペアをたくさん用意して巻き付けていく。
この方法でうまくいきます。
具体例を挙げましょう。
数字 \(1\) から \(49\) までの7×7サイズの同心方陣です。
中央を \(25\) にして、足して \(50\) になるペア24組を巻き付けているわけですね。