弦に注目してみましょう
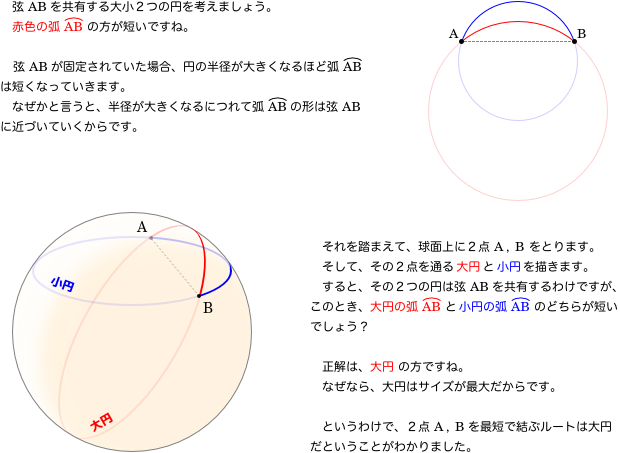
球面上の2点を通る大円を描くと、その大円は2点間の最短ルートを作ります。
なぜでしょう?
「点Bに立って、点Aの方向を向いたまま球面を真っ直ぐ歩くと、軌跡は円弧だ」と直感的にわかりそうなので、2点を結ぶ円弧ルートに限定して話を進めます。
(2022. 7.13. 追記)
2点A, Bを結ぶ曲線は円弧に限りません。
「く」の字に曲がったり「S」字に波打ったりも可能なので、上記は本当は証明になっていません。
実際は、積分を使って非常に難しい証明を展開することになります。
当サイトはあくまで「パズル系」ですので、難解な話からは逃げようと思います😅
「点Bに立って、点Aの方向を向いたまま球面を真っ直ぐ歩くと、大円をたどって最短だ」くらいのイメージだと理解しやすいかも。
更新履歴
- 2022. 7.11.
- 新規公開。
- 2022. 7.13.
- 説明の足りなかったところを追記。