足し算で表せば一発です
なぜタテヨコかぶらない数字5個の合計は65になるんだろう?
その証明です。
図1
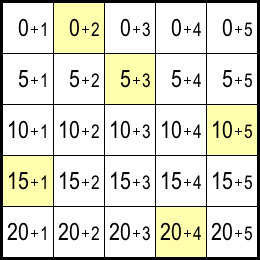
図1のように、順番に並んだ数字1〜25を足し算で表しちゃいましょう。
この足し算には次の特徴があります。
- 0, 5, 10, 15, 20 はそれぞれヨコ1列に並んでいる。
- 1, 2, 3, 4, 5 はそれぞれタテ1列に並んでいる。
これを踏まえて、タテヨコかぶらない5マスを任意に選んでみましょう。
例えば、図1の黄色5マスのように。
そして、その5マスの和を考える。
その和について、こういうことが成り立つんです。
- タテヨコかぶらない5マスをどのように選んでも、その和は 0, 5, 10, 15, 20, 1, 2, 3, 4, 5 の総和になっている。
たしかに、各ヨコ列に黄色マスは1個しかないのだから、0, 5, 10, 15, 20 は1回ずつしか選ばれない。
各タテ列も同様で、1, 2, 3, 4, 5 は1回ずつしか選ばれない。
だから、黄色マスの合計は 0, 5, 10, 15, 20, 1, 2, 3, 4, 5 の総和になる。
その総和は 0+5+10+15+20+1+2+3+4+5=65 です。
したがって、タテヨコかぶらない数字5個の合計は必ず65になるんですね。