実は折れ曲がっていた
変形前の正方形は4つの図形に分割されています。
台形が2つ、直角三角形が2つですね。
実は、変形後の長方形において台形a, bを正確なサイズで描いた時、直角三角形c, dに対しておかしなことが起こるんです。
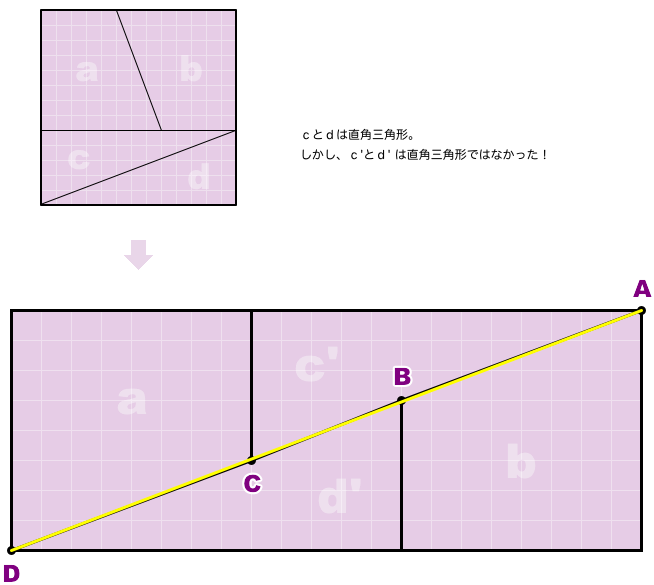
長方形を拡大して、2点A, Dを直線(黄色)で結んでみました。
黄色い線と黒い線がほんの少しずれているのがわかるでしょうか。
実は、点Bも点Cも黄色い線からほんの少しずれた位置にあるんですね。
点Bは黄色線より上、点Cは黄色線より下。
4点A~Dを通っている一筋の線、これは直線ではありません。
ほんの少しジグザグに曲がっているんです。
ということは……、c' もd' も直角三角形ではなかったということか!
まるで直角三角形のように振る舞っていたc' とd'。
実は、cとdに激似のそっくりさんだったというわけです。
いや〜、これは騙されるわ😓
更新履歴
- 2022. 2. 5.
- 以前公開していたものを加筆して再公開。