1.ほんの少〜しふくらんでいる
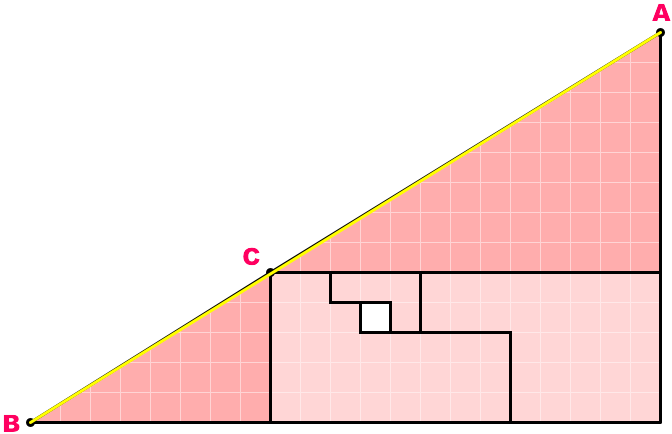
図を拡大して、2点A, Bを直線(黄色)で結んでみました。
黄色い線と黒い線がほんの少しズレているのがわかるでしょうか。
実は、点Cは黄色い線よりほんの少し左上に位置しているんですね。
3点A, B, Cは一直線上にありません。
パッと見て直角三角形に見えるこの図形、本当は三角形ではなかった!
正しくは四角形なのです。
「直角三角形が微妙にふくらんでいる」という感じの四角形なんですね。
2.ほんの少〜しヘコんでいる
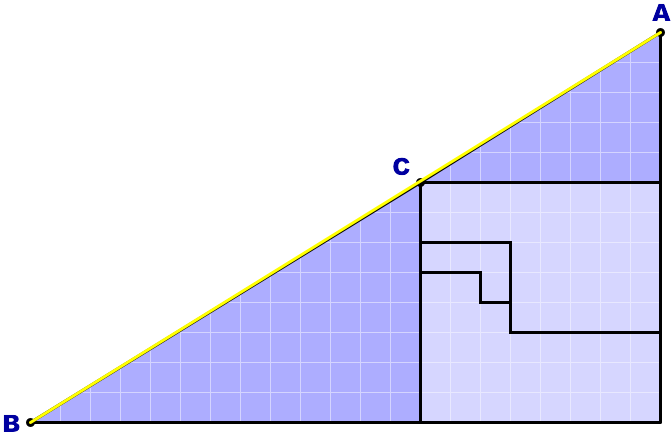
同様に、図を拡大して2点A, Bを直線(黄色)で結んでみました。
この図でも黄色い線と黒い線がほんの少しズレています。
今度は、点Cは黄色い線よりほんの少し右下に位置しているんですね。
3点A, B, Cは一直線上にありません。
上図と同様、この図形も直角三角形ではありません。
れっきとした四角形です。
微妙にヘコんだ三角形モドキといったところでしょうか。
つまり、パッと見で同じ図形に見えるのに、微細なふくらみと微細なヘコみという違いがあったんですね。
だから、当然、この2つの図形は面積が異なります。
その違いというのが、セクション1の画像にある白い小さな四角形の面積であるというわけなんです。
更新履歴
- 2022. 2. 5.
- 以前公開していたものを加筆して再公開。